מה סוד קסם הריבוע הנעלם?
ברשת האינטרנט (ובפייסבוק כמובן) רץ שוב ושוב ושוב "פרדוקס" שטח שהוא למעשה אשליית ראיה.
 |
| התמונה נוצרה על ידי Daniel Takacs. |
מדובר בשעשוע מתמטי שהוא אשליית ראייה שמיוחסת לקורי (שעליו נכתב באריכות אצל מרטין גרדנר, ו-גם אצל פרדריקסון).
מה יש פה בכלל? מה הפרדוקס?
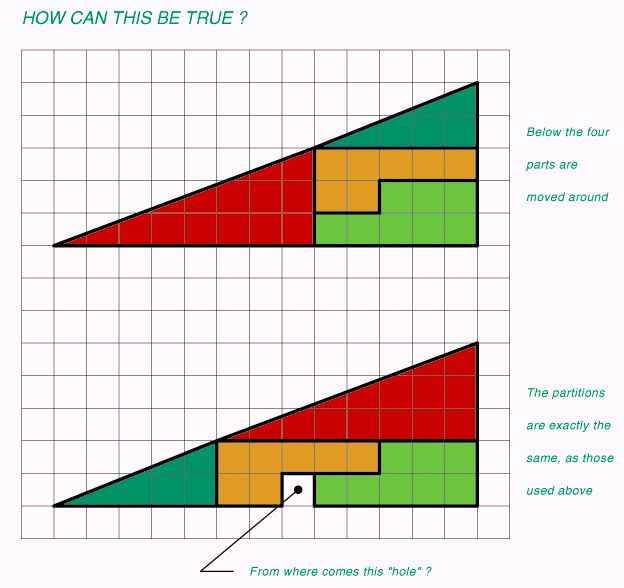
בתמונה רואים שתי צורות מורכבות: אחת מעל השנייה. שתי הצורות המורכבות בנויות מאותן 4 צורות: משולש ישר זוית כחול, משולש ישר זוית אדום, ושני משושים בצורת מדרגה: אחד צהוב ואחד ירוק. הבעיה היא שבעוד שאנו מצפים לשימור שטח, ז"א שהשטח הכולל של המצולעים שמרכיבים את הצורות המורכבות ישאר זהה ללא קשר לאופן שבו משלבים את הצורות הללו ביחד, מראים לנו שבסידור העליון מתקבלת יחידת שטח אחת יותר מאשר בסידור התחתון. אז הפרדוקס הוא של שימור שטח.
אז איך זה יכול להיות?
אז זהו, שזה לא באמת יכול להיות. אין פה פרדוקס. יש פה אשליית ראייה. שימו לב שבשני המקרים יש שני משולשים ישרי זוית: הכחול והאדום. הכחיל בעל ניצב שאורכו שתי יחידות אורך וניצב שאורכו 5 יחידות אורך. האדום בעל ניצב שאורכו 3 יחידות אורך וניצב אחר בעל 8 יחידות אורך. המסקנה היא שהזוית שבין היתר לבין הניצב האופקי בשני המשולשים אינה אותה הזוית (אם כי היא נראית אותה הזוית). השיפועים שונים: 2/5 במשולש הכחול ו-3/8 במשולש האדום. כמובן, השברים הללו אינם שווי ערך. מדוע זה חשוב? זה חשוב כי בעצם הצורה המורכבת שמופיעה בחלקו העליון של הציור אינה משולש ישר זוית אלא מרובע!!
 |
| התרשים מתוך הרשימה המצויינת של גדי אלכסנדרוביץ בנושא בבלוג שלו "לא מדויק" |
האם יש דרך קלה לייצר עוד אשליות שכאלה?
כן! הגדלים היסודיים בבעיה שלפנינו הם: 2, 3, 5, 8, 13 ... אלה מספרים רצופים בסדרת פיבונאצ'י.
המורה,
כמובן, שגדי אלכסנדרוביץ כבר כתב על זה רשימה:
השבמחקhttp://www.gadial.net/2007/10/24/triangle_illusion/